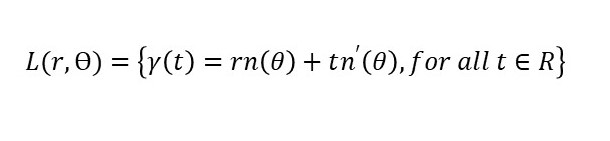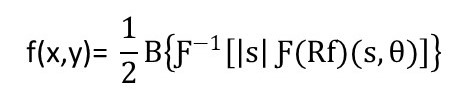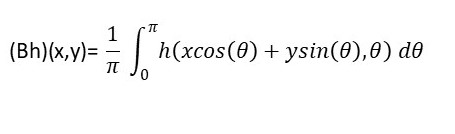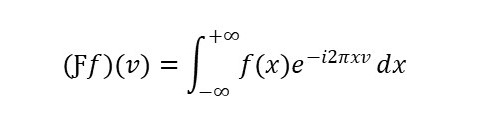Have you ever wondered how could doctors reproduce images of internal parts of the human body? Have you undergone a medical treatment for which a CT exam was required and -out of curiosity- would like to know what’s behind this medical technology?
Well, the fundamental problem of this procedure is essentially mathematical, and I will try in this article to give some insights into the intriguing math behind it.
First, let me state some historical facts. In 1979 Allan Cormack and Godfrey Hounsfield were awarded the Nobel Prize for Medicine and Physiology for the development of this groundbreaking medical technology. Cormack exposed in one of his papers an algorithm to create an image from X-ray data, while Hounsfiled – a research scientist at EMI Central Research laboratories in the United Kingdom – designed the first operational CT scanner. But the Mathematical theory behind it dates back to 1917 when the Austrian Mathematician formulated the so-called Radon transform.
So how did the Radon Transform help the two pioneering scientist-engineers in formulating the image reconstruction algorithm? I’ll start from the beginning.
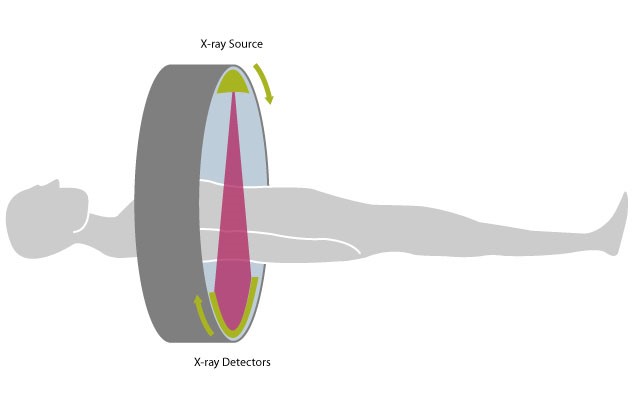
A patient is being placed under the scanner like in the figure 1 (1).
An X-ray source emits a fan of beams which penetrate the body at various angles. A detector on the opposite side of the source will be impacted by the arriving beams. Therefore, a CT scanner makes two measurements: the initial intensity of each X-ray beam, and the final intensity of each X-ray beam. The loss in intensity of the single beam gives information about the internal density of the body. We would like then to use these measurements in order to get a picture of the varying densities.
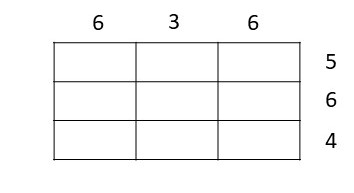
Does this approach look somehow familiar to you? This is exactly what is called inverse problem, and to understand better this process forget for a while about medical imaging and consider the popular killer Sudoku. It’s an advanced version of Sudoku, but here the player must fill the grid with numbers from 1 to 9 such that the sum of all numbers matches a given number. For example:
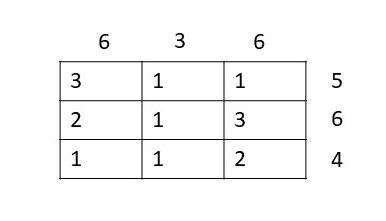
A possible solution for it could be the following:
It might sound surprising, but this is exactly the problem of image reconstruction. The X-ray encounters different materials along its path (blood, bones, etc), and each one will absorb different quantities of its energy. But what is being measured by the CT scan is only the final loss of energy at the end of the path. Here comes the challenging task: given the final sum, recover the local loss of energy. For the sake of clarity, the analogy between them is presented in parallel in the following table:
From a mathematical point of view, the reconstruction can be done through two steps:
- The Radon transform;
- Inversion of the Radon transform;
The Radon transform
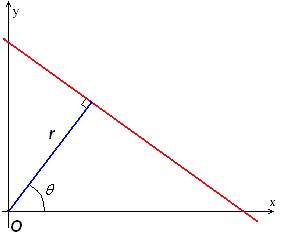
We consider a parallel beam geometry, where each X-ray can be represented in the x-y plane as a line. In order to capture also vertical lines, we adopt, instead of the cartesian coordinates, a point-normal parametrization of the line: each one is uniquely determined by the distance r from the origin, and the angle Ѳ as showed in the figure 2:
A generic line can be then parametrized as
Where n is the the normal to the line in the point determined by the angle , and n’ is the corresponding tangent vector.
It’s possible now to define the radon transform (Rf)(r,θ) : Given a function f , for any pair (r, θ), is defined as (2)
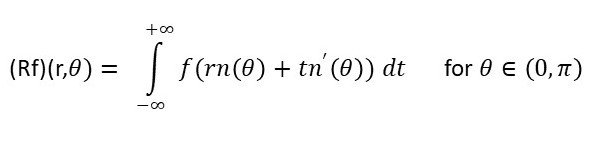
This is a line integral. It involves functions evaluated on a certain path, which is in our application the straight line of the X-ray beam.
In this definition the function f(x,y) represents our density attenuation coefficient function: it’s the unknown. And on the left hand side of the formula, (Rf)(r,θ) , is the information we collect from the measurements of the detector. Therefore, this formula gives back the overall loss of intensity of one single X-ray, after it crosses the body. We can then rephrase the fundamental question of image reconstruction as following:
Can we recover the function f(x,y) if we know the values of the Radon transform
for each line?
Inversion of the Radon transform
In the second step we provide a formula for the recovery of the attenuation function, given the radon transform of the object. The following theorem gives the exact reconstruction formula.
For an absolutely integrable function f (namely the integral of its absolute value is finite) it holds:
- B is the back-projection operator, defined for a generic function h(t,θ ) as:
- Ƒ is the Fourier transform which is defined for a given absolutely integrable function f on R as:
- s is a filtering.
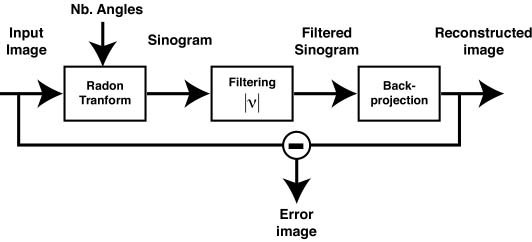
This formula gives a complete answer to our question. To get the reconstruction we need to apply this particular combination of operators (or transforms): we first perform the Fourier transform of the Radon data, and we filter it to keep low the noise level; we apply then the inverse Fourier transform to it. The final step is to perform the Back projection operator. The essential part of this formula is the filtering: without it, we are left with the inverse Fourier multiplied by the operator itself, so they cancel out each other. And the formula reduces only to the back projection of the radon data, which does not reproduce the function f(x,y). The whole process can be summarized in the following block-diagram representation (3) :
This was a quick overview of the most important steps in the mathematics behind medical imaging. A lot of work still has to be done. First, I would like to point out that the formula described above requires an infinite number of measurements, whereas CT scanners can provide only a finite number of them. Passing from the infinite (or continuous) representation to the corresponding finite one (or discrete) is a very common process in applied mathematics, since we deal only with finite quantities when solving real world problems. For instance, when solving a differential equation that models a certain physical phenomenon, we need to discretize the equation, in order to give it to the computer, which can only deal with finite dimensional vectors and matrices.
This is not the end of the story. Other techniques have been developed such as the magnetic resonance imaging (MRI), positron emission tomography (PET) and single photon emission computed tomography (SPECT). Each method has its advantages in terms of image resolution ad safety, and many researchers are trying to develop new techniques and build more sophisticated CT scanners to detect specific diseases and life-threatening conditions. I personally consider the medical technology as one of the most beneficial advances of our time, and hope I was able to deliver a feeling of how mathematics has become central in everyday life, but could even do more: save a lot of lives.
REFERENCES
(1): image taken from
(2): This definition comes from beer’s law. An extended treatment can be found in the provided reference book, chapter 1.2.
(3): image taken from http://bigwww.epfl.ch/demo/jtomography/
(4): image taken from http://www.radiologia-sapienza.it/Tc_Torace.html
Reference book:
“The mathematics of medical imaging “ by Timothy G. Feeman.